Bộ lọc thụ động thông thấp RC

Một bộ lọc thông thấp cho phép các tần số thấp hơn một tần số cắt nhất định đi qua và suy giảm những tần số cao hơn tần số đó.

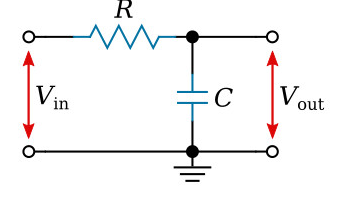
Mạch đầu tiên chúng ta sẽ phân tích là mạch bộ lọc thông thấp RC, như hình trên. Trước khi đi vào phân tích toán học, chúng ta có thể suy ra một số tính chất điện từ bằng cách quan sát mạch.

Nếu điện áp đầu vào có tần số rất thấp, độ phản kháng của C sẽ rất cao so với R, và C có thể được coi là mạch hở. Do đó, ở các tần số thấp, điện áp đầu vào V sẽ xuất hiện gần như không bị suy giảm ở đầu ra. Từ đó có tên gọi bộ lọc thông thấp. Khi tần số đầu vào tăng lên, độ phản kháng _X_C trở nên nhỏ hơn, khiến đầu vào bị suy giảm ngày càng nhiều. Ở tần số vô cùng cao, _X_C = 0 và do đó điện áp đầu ra _V_out = 0.

Để phân tích mạch một cách toán học, chúng ta sẽ sử dụng mối quan hệ phân áp điện và viết

Tuy nhiên, chúng ta sẽ giải tỷ lệ của Vout trên Vin, vì thông thường chúng ta muốn biểu thị lợi nhuận hoặc tổn thất của bộ lọc. Tỷ lệ này được gọi là hàm truyền. Với hàm truyền, chúng ta có:

trong đó _ω_C = 1/RC là tần số đặc trưng.

Hàm truyền có thể được biểu diễn dưới dạng cực:

Đáp ứng tần số

Một cách hiệu quả nhất để thể hiện đặc tính tần số của một bộ lọc là vẽ đồ thị biên độ của hàm truyền (đặc tính biên độ) so với tần số trên một đường cong và đặc tính pha trên một đường cong riêng biệt nhưng cùng trục tần số. Đặc tính biên độ, có thể thay đổi trong một phạm vi rộng, có thể được vẽ một cách thuận tiện theo đơn vị dB. Các đường cong với loại hiển thị này được gọi là đồ thị Bode và được ứng dụng rộng rãi trong phân tích mạch AC.

Đặc tính Biên độ

Trước hết, xét đặc tính biên độ (phổ) tương ứng với phương trình trên. Đây là giá trị tuyệt đối (biên độ) của hàm truyền, hay

Trên cơ sở dB, điều này trở thành

Hãy xem xét phương trình trên ở tần số rất thấp và rất cao. Đối với tần số thấp, ta có

Như vậy, đặc tính tần số thấp về cơ bản không phụ thuộc vào tần số và có thể được biểu diễn bằng một đường thẳng ngang ở 0 dB như trong hình dưới đây. Đặc tính biên độ thực tế cho bởi hàm truyền là đường tiệm cận với đường thẳng này ở tần số nhỏ ω.

Đối với trường hợp cực đoan khác, ta có

Đây là dạng G_dB = -20_x, trong đó x = log10 (ω/_ω_C). Đường thẳng được xác định là đường tiệm cận tần số cao của đặc tính thực tế. Độ dốc của đường tiệm cận là _dG_dB/dx = -20; nghĩa là, khi x tăng một đơn vị, _G_dB giảm 20 dB. Nhưng

và vì vậy ω/_ω_C phải tăng gấp 10 lần, hay một thập phân, để làm x tăng một đơn vị. Do đó, độ dốc của đường tiệm cận tần số cao là -20 dB trên thập phân. Một số người thích sử dụng đơn vị octave (tỷ lệ tần số 2:1). Độ dốc tương ứng là -6 dB trên octave. Hai đường tiệm cận thẳng giao nhau tại ω/_ω_C = 1, vì lúc đó đặc tính biên độ có giá trị bằng 0. Hai đường tiệm cận được vẽ đứt nét trong hình trên. Điểm giao của chúng, ω = _ω_C, ngoài việc được gọi là tần số đặc trưng của mạch, cũng được gọi là điểm gãy hay tần số cắt. Cả hai đường tiệm cận hình thành một xấp xỉ đường gãy cho đặc tính thực tế. Tùy thuộc vào độ chính xác mong muốn, có thể không có đường nào đủ tốt để xấp xỉ đặc tính thực tế trong lân cận của ω = _ω_C. Có thể chứng minh rằng sai số lớn nhất xảy ra tại ω/_ω_C = 1 và xấp xỉ 3 dB. Hơn nữa, cách điểm này một octave (tại ω/_ω_C = 0,5 và ω/_ω_C = 2) sai số xấp xỉ 1 dB. Từ đó, ta có thể vẽ đặc tính biên độ thực tế với độ chính xác hợp lý. Đặc tính thực tế được thể hiện bằng đường liền nét trong hình trên. Đặc tính thông thấp của mạch được thấy rõ trong hình này.

Đặc tính Pha

Bây giờ, hãy xem xét góc của hàm truyền của bộ lọc (đôi khi được gọi là phổ pha), là

Góc pha bắt đầu từ 0 cho ω = 0 và tiến dần đến -π/2 radian ở ω lớn. Đặc tính pha có thể được xấp xỉ khá tốt bởi ba đoạn thẳng, như minh họa trong hình dưới: một xấp xỉ tần số thấp ở 0 radian, một xấp xỉ tần số cao ở -π/2 radian và một xấp xỉ tần số trung gian tiếp tuyến với đường cong tại -π/4 radian. Có thể chứng minh rằng đoạn giữa giao với xấp xỉ tần số thấp tại ω/_ω_C = 1/4,81 và giao với xấp xỉ tần số cao tại ω/_ω_C = 4,81. Đặc tính thực tế được thể hiện bằng đường liền nét trong hình.