Hướng dẫn Mạch trừ toàn phần và Mạch trừ bán phần
Mạch trừ toàn phần
Mạch trừ toàn phần thực hiện phép trừ của hai bit, một bit là số bị trừ (minuend) và bit kia là số trừ đi (subtrahend). Trong mạch trừ toàn phần, ‘1’ được vay từ bit số bị trừ kề cận thấp hơn. Do đó, có ba bit được xem xét ở đầu vào của một mạch trừ toàn phần. Có hai đầu ra, đó là đầu ra HIỆU D và đầu ra BORROW Bo. Đầu ra BORROW cho biết bit số bị trừ cần vay ‘1’ từ bit số bị trừ kế tiếp.
Bảng chân lý
| A (Minuend) | B (Subtrahend) | Bin (Borrow in) | D (Hiệu) | Bo (Borrow out) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Sơ đồ Karnaugh
- Sơ đồ Karnaugh cho đầu ra HIỆU D:
Không có đơn giản hóa có thể thực hiện cho đầu ra HIỆU D.
Biểu thức cho D:D = A'B'Bin + A'BC' + AB'C' + ABC - Sơ đồ Karnaugh cho đầu ra BORROW Bo:
Có thể đơn giản hóa biểu thức cho đầu ra BORROW Bo.
Biểu thức đơn giản cho Bo:Bo = A'BC + AB'C + ABC'
Thiết kế mạch
Mạch trừ toàn phần có thể được thiết kế bằng cách sử dụng các cổng logic cơ bản như XOR, AND và OR theo các biểu thức logic ở trên.
So sánh với mạch cộng toàn phần
Khi so sánh biểu thức của mạch trừ toàn phần và mạch cộng toàn phần, ta thấy rằng:
- Biểu thức cho đầu ra HIỆU D giống với biểu thức cho đầu ra TỔNG của mạch cộng toàn phần.
- Biểu thức cho đầu ra BORROW Bo của mạch trừ toàn phần giống với biểu thức cho đầu ra CARRY-OUT Co của mạch cộng toàn phần.
Thiết kế mạch trừ toàn phần bằng mạch trừ bán phần
Trong mạch trừ bán phần, đầu vào A được bù. Do đó, mạch trừ toàn phần có thể được thiết kế bằng cách sử dụng hai mạch trừ bán phần và một cổng OR.

Mạch trừ nhị phân 4 bit
Mạch trừ nhị phân 4 bit có thể được triển khai bằng cách sử dụng các mạch trừ toàn phần. Đầu vào là A0, A1, A2, A3 (số bị trừ) và B0, B1, B2, B3 (số trừ đi). Bin là bit nhớ vay vào. Đầu ra là HIỆU D0, D1, D2, D3 và Bout là bit nhớ vay ra.Mạch trừ toàn phần giúp thực hiện phép trừ nhị phân đầy đủ bằng cách xử lý bit nhớ vay từ các vị trí có trọng số thấp hơn. Nó được sử dụng rộng rãi trong các ứng dụng xử lý số học và tính toán số học.

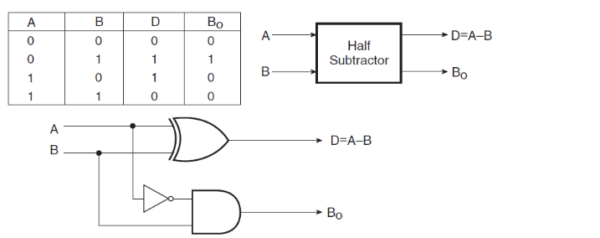
Mạch trừ bán phần (Half-Subtractor)
Phép trừ được thực hiện theo cột tương tự như hệ thống số thập phân. Trong bước đầu tiên, chúng ta trừ các bit LSB (bit trọng số thấp nhất) và di chuyển về phía MSB (bit trọng số cao nhất). Bất cứ khi nào số trừ đi (subtrahend) lớn hơn số bị trừ (minuend), chúng ta vay từ vị trí bit cao hơn kế tiếp có giá trị ‘1’.Ví dụ dưới đây minh họa các bước khác nhau khi trừ (1001) từ (1100).
Ở đây, 1 được vay từ vị trí MSB thứ hai, để lại 0 tại vị trí đó. Số vay được đưa đến vị trí MSB thứ ba để tạo thành 10. Trong số 10 tại vị trí này, 1 được đưa đến vị trí LSB để tạo thành 10 tại đó, để lại 1 tại vị trí MSB thứ ba.10 – 1 trong cột LSB cho kết quả 1, 1 – 0 trong cột MSB thứ ba cho kết quả 1, 0 – 0 trong cột MSB thứ hai cho kết quả 0 và 1 – 1 trong cột MSB cũng cho kết quả 0 để hoàn tất phép trừ.
Phép trừ các số hỗn hợp cũng được thực hiện theo cách tương tự.Trong mạch số, một cách để thực hiện phép trừ hai số nhị phân là cộng bù 2 của số trừ đi với số bị trừ. Điều này cho thấy rằng phép trừ có thể được thực hiện bằng cách sử dụng các mạch cộng. Trong phần này, chúng ta sẽ xem xét các mạch trừ bán phần và trừ toàn phần, tương ứng với mạch cộng bán phần và cộng toàn phần.Mạch trừ bán phần chủ yếu được sử dụng để trừ một chữ số nhị phân từ một chữ số khác để tạo ra đầu ra HIỆU và đầu ra BORROW. Đầu ra BORROW ở đây chỉ ra liệu có vay ‘1’ để thực hiện phép trừ hay không.
Bảng chân lý
| A (Minuend) | B (Subtrahend) | D (Hiệu) | Bo (Borrow out) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
Sơ đồ Karnaugh
- Sơ đồ Karnaugh cho đầu ra HIỆU D:
Không có đơn giản hóa có thể thực hiện cho đầu ra HIỆU D.
Biểu thức cho D:D = A'B + AB'(Cổng XOR) - Sơ đồ Karnaugh cho đầu ra BORROW Bo:
Có thể đơn giản hóa biểu thức cho đầu ra BORROW Bo.
Biểu thức đơn giản cho Bo:Bo = A'B(Cổng AND với đầu vào A bù)
Thiết kế mạch
Mạch trừ bán phần có thể được thiết kế bằng cách sử dụng một cổng XOR cho đầu ra HIỆU D và một cổng AND với đầu vào A bù cho đầu ra BORROW Bo.

So sánh với mạch cộng bán phần
Khi so sánh mạch trừ bán phần với mạch cộng bán phần, ta thấy rằng:
- Biểu thức cho đầu ra HIỆU D giống với biểu thức cho đầu ra TỔNG của mạch cộng bán phần.
- Biểu thức cho đầu ra BORROW Bo của mạch trừ bán phần tương tự với biểu thức cho đầu ra CARRY của mạch cộng bán phần, nhưng với đầu vào A bù.
Mạch trừ bán phần được sử dụng để thực hiện phép trừ nhị phân đơn giản giữa hai bit. Tuy nhiên, nó có giới hạn vì không xử lý số nhớ vay từ các vị trí có trọng số thấp hơn. Để khắc phục điều này, ta sử dụng mạch trừ toàn phần.